Aşağıdaki figürdeki gibi basit bir hücre düşünün: A metaboliti hücreye b1 hızında girebiliyor ve bu metabolit hücre içerisinde sırasıyla v1 ve v2 hızlarında B ve C metabolitlerine dönüşebiliyor. Aynı anda C metaboliti v3 hızında A’ya geri dönüşebiliyor. Tabii bütün bu dengeyi enzim kinetiklerini hesaba katmadan ve kütle dengesinin sağlandığını varsayarak kurmalıyız (bu cümle yazının devamında daha anlamlı hale gelecektir).
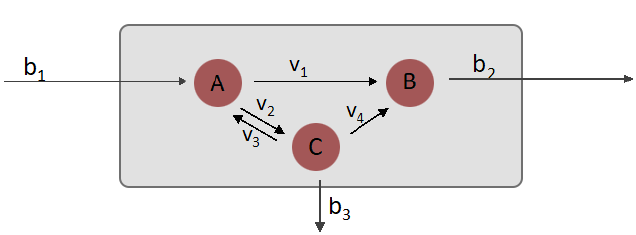
Yapacağımız diğer bir varsayım da hücrenin steady-state (kararlı durumda) olduğudur. Bu varsayımımız üzerine A metaboliti üzerinden geçen bütün reaksiyonları bilir hale geliyoruz ve A’nın üretildiği hızda tüketildiğini kabul ettiğimiz için aşağıdaki diferensiyel denklemi yazabiliyoruz:
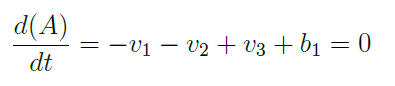
Diğer bir deyişle, yukarıdaki denklemi yazarak hücre içerisinde A metabolitinin birikmeyeceğini kararlaştırmış olduk. Aynı denklemi B ve C metabolitleri için de yazarsak, 3 metabolit ve 7 reaksiyonlu bu diferensiyel denklemleri doğrusal denklem sistemi halinde ifade edebiliriz:
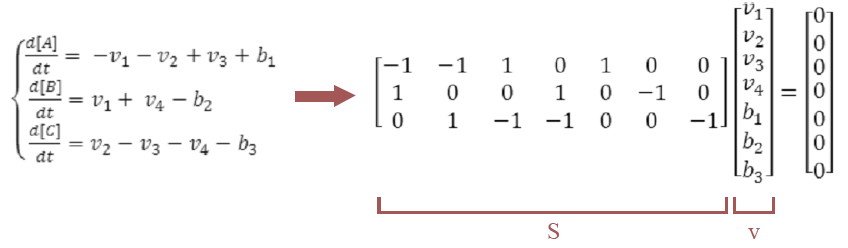
İfade ettiğimiz doğrusal denklem sistemini biraz daha açıklayalım: Oluşturduğumuz matrikste reaksiyonların stokiyometrik katsayılarını barındırıyoruz, bu matrikse “S matriksi” diyeceğiz. S matriksinin her bir sütunu tek bir reaksiyonu temsil ederken bu reaksiyona katılan metabolitler arasındaki bağlantılar hakkında bize bilgi verdiğini görebiliyoruz. Benzer şekilde, S matriksinin her bir satırı ise, bir metabolitin katıldığı tüm reaksiyonlar hakkında bilgi veriyor. S matriksinin yanında gördüğümüz vektör ise bizim flux (akı) vektörümüz, metabolitlerin konsantrasyon değişikliklerini barındırıyor. Diğer bir deyişle, flux vektörü her metabolitin zamana bağlı akış hızını temsil ediyor.
Biyolojik ağlardaki reaksiyon sayısının büyüklüğünü düşündüğümüzde, bu sistemleri matematiksel olarak ifade ettiğimizde oluşacak S matriksinin boyutunun hayli büyük olacağını ve çoğunlukla 0 barındıracağını öngörebiliriz. Reaksiyon sayısının çok olması doğrusal denklem sistemini kararsız (underdetermined) hale getirir ve bu sistemlerin tek bir çözümü yoktur.
Modeli Kısıtlamak
Yukarıda bahsettiğimiz gibi, metabolik sistemlerin çözüm kümesi özgün değildir, yani S . v = 0 eşitliğini sağlayan birden fazla v vektörü bulunabilir. Biyolojik olarak daha anlamlı sonuçlar elde edebilmek için v vektörünü kısıtlandırılmış bir uzay içerisinden hesaplayabiliriz. Bu kısıtlamadan kastımız, biyolojik sistemlerin doğada uymak zorunda olduğu kuralların (kimyasal dengeler, termodinamik yasalar gibi) modelin çözüm kümesini daraltacak şekilde uygulanmasıdır.
Elle tutulur bir örnek vermek gerekirse, biyolojik sistmelerin fiziko-kimyasal özelliklerini düşündüğümüzde kütle ve yük dengesinin kurulması gerektiğini biliriz. Bu dengenin sağlanması için sisteme “zorunlu kısıtlama”lar getirmek kaçınılmaz olur. Örneğin bir reaksiyonun hangi yönde gerçekleştiği termodinamik yasalar ile belirlenmiştir. Bu reaksiyonlar matematiksel olarak sadece pozitif (vi ≥ 0, ileri yönde) ya da sadece negatif (vi ≤ 0, geri yönde) değerler alacak şekilde çözüm kümesini daraltabilir.
Başka bir kısıtlama örneği olarak deneylerin gerçekleştirildiği çevresel koşullar veya kültür medyasındaki değerlerin sisteme tanıtılması verilebilir. Hücre içerisine girebilecek besin miktarı (karbon, oksijen gibi) biliniyorsa, flux vektörü de o doğrultuda kısıtlandırılmalıdır.
Flux vektörünü kısıtlamak için pek çok yöntem kullanılabilir. Güncel çalışmalar protein miktarı, enzimatik aktivite, transkripsiyon miktarı gibi yeni nesil teknolojilerin sağladığı verileri de modelleri kısıtlamak için kullanmaktadır.
Flux Balance (Akı Denge) Analizi
Flux Balance Analizi (FBA), hücrelerin bir amaca doğru hayatlarını optimize ettiklerini öne sürer ve metabolik sistemleri bu doğrultuda çözmeye çalışır. Birden fazla sonuç içerisinden doğru flux vektörünü verebilmek için sisteme, genelde “büyüme reaksiyonu” olarak anılan, bir objektif fonksiyon dahil edilir. Bu büyüme reaksiyonu modellediğiniz hücreden hücreye farklılık gösterecektir. Genel hatlarıyla hücrenin biyokütle üretebilmesi ve üreyebilmesi için gerekli metabolitleri içeren son tüketim yeri olarak tanımlanır.
Matematiksel olarak anlatmak gerekirse, FBA aşağıdaki doğrusal problemi çözmeye çalışır:
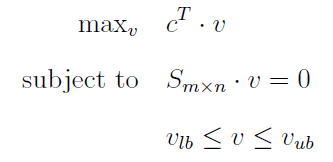
Bu denklemlerde c objektif fonksiyon vektörü, v flux vektörü ve S stokiyometrik matrikstir. Flux vektörünü sınırlayan vlb ve vub vektörleri, her bir fluxın alabileceği minimum (lower bound) ve maksimum (upper bound) değeri kısıtlayan vektörlerdir.
FBA, kısıtlandırılmış çözüm kümesi içerisinden objektif olarak tanıttığımız reaksiyonun maksimum değerini veren özgün vektörü bize sonuç olarak sunar. Bu sonucun biyolojik olarak anlamlılığı, objektif fonksiyon olarak ne tanımladığımıza bağlı olarak değişir.
Referanslar
- Pinzon, W., et al. “Mathematical Framework Behind the Reconstruction and Analysis of Genome Scale Metabolic Models.” Archives of Computational Methods in Engineering 26.5 (2019): 1593-1606.
- Orth, J. D., Thiele, I., & Palsson, B. Ø. (2010). What is flux balance analysis?. Nature biotechnology, 28(3), 245-248.
Bu yazıda metabolizmanın matematiksel modellenmesi üzerine kullandığım terimleri olabildiğince basitleştirmeye ve konu hakkında hiçbir bilgisi olmayan bir kişinin anlayabileceği bir şekilde açıklamaya çalıştım. Umarım başarılı olabilmişimdir. Konu hakkında Türkçe kaynak az olduğu için bu dilde yayınlamayı tercih ettim. İlgisini çekenlere referanslarda belirttiğim, okuması gerçekten kolay ve eğlenceli olan iki makaleyi kesinlikle okumalarını öneriyorum. Kendinize iyi bakın!
